CubeSat Detumbling Algorithm Research Project
Project Goal:
To design an algorithm that would perform attitude determination and control on a student-built CubeSatellite in low Earth orbit.
Technical Skills Involved:
- Embedded Systems
- Satellite Control Algorithms
- Satellite Simulations in MATLAB/python
Other Skills Involved:
- Long term project organization
- Self-teaching complicated technical concepts
- Presentation/report writing skills

Results
Over the course of the summer, I was able to fully flesh out and simulate the majority of this algorithm. I am now continuing to finalize my design as the Attitude Determination and Control System (ADCS) subteam lead within the organization.
Technical Overview:
For this project, I was tasked with using the CubeSatellite’s hardware to create a reliable control system, and simulating the efficacy of that system. For attitude determination, the CubeSat’s main sensors are a magnetometer and a sun sensor. For attitude control, the CubeSat has an actively-controlled magnetorquer and a passive gravity gradient boom (GGB). The algorithm that I developed relies on different phases to deal with the topic of detumbling:
- Phase 0 occurs when angular velocity is above a certain threshold and relies on natural eddy currents to dissipate rotational energy.
- Phase 1 describes the reduction of the CubeSat’s rotational velocity through the use of the B-dot algorithm by which magnetorquers are used to counteract rotations observed by the magnetometers.
- Phase 2 describes the pointing of the CubeSat and relies on the TRIAD algorithm to calculate the current orientation from the magnetometer, sun sensor, and position data.
- Phase 3 describes the extension of the GGB which should cause the further reduction of angular velocity and the addition of a passive restorative force on the CubeSat’s rotation. I established very specific criteria for the beginning of this extension and various safeguards to ensure that the extension doesn’t cause the CubeSat to enter a dangerous state.
- Phase 4 involves the utilization of the B dot algorithm with a lower gain value to continue damping out oscillatory motion while reducing power consumption.
My project involved also creating a MATLAB program that would incorporate the detumbling algorithm into a simulation of the CubeSat’s dynamics. I also wrote several python scripts to analyze the physics at play with the passive stabilization caused by the GGB.
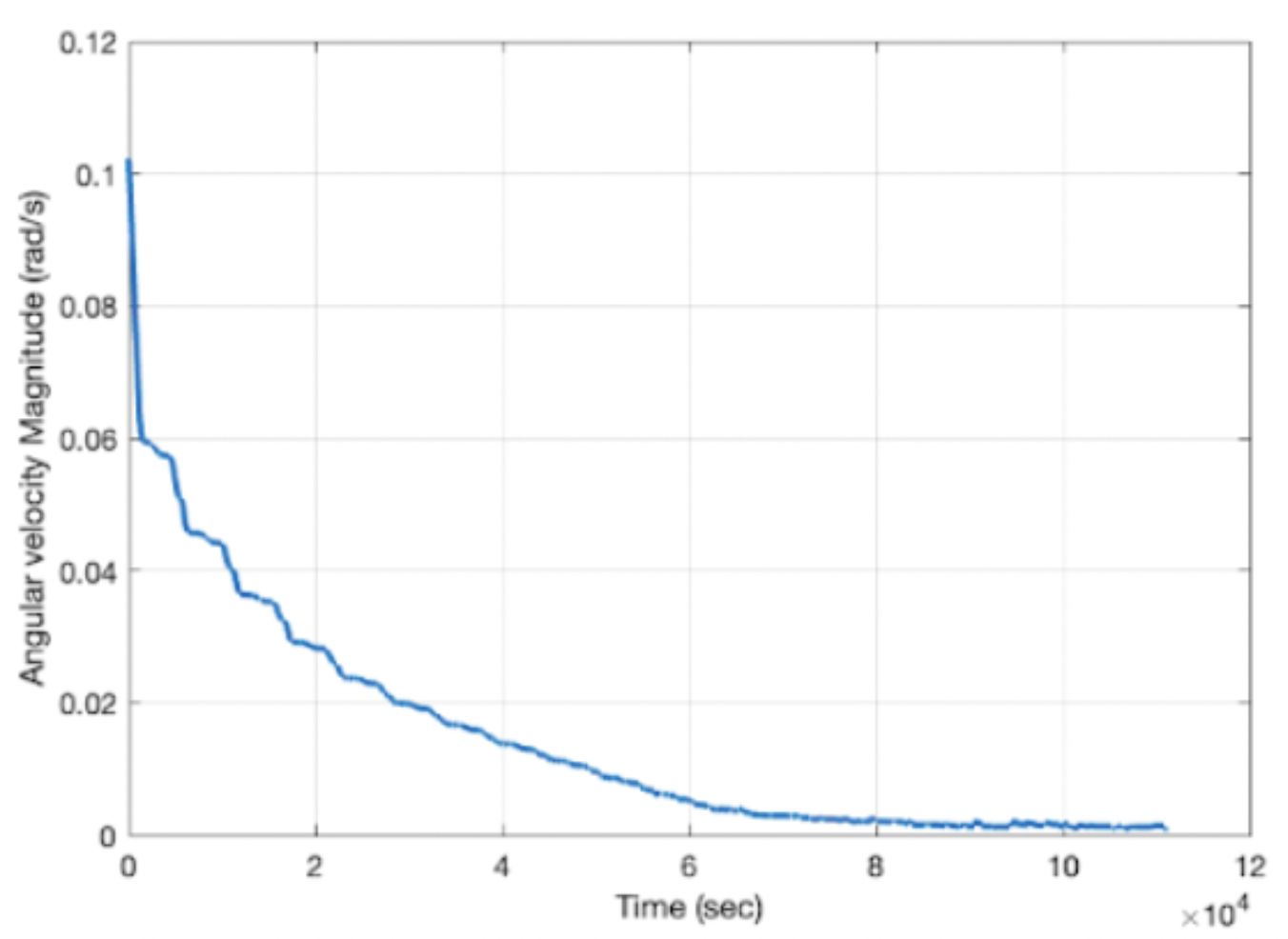
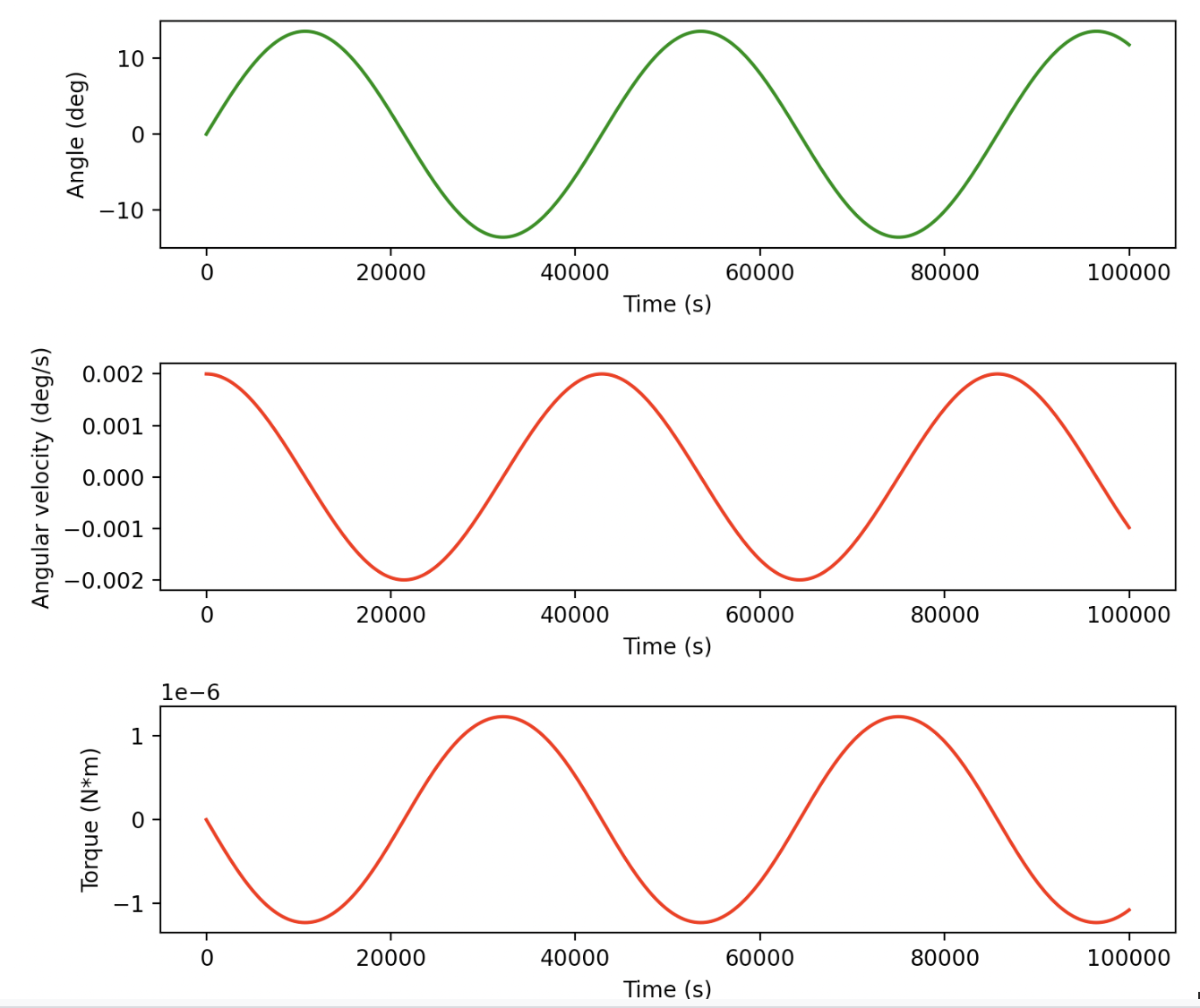
Project Process:
Since the beginning of my first year, I have been a part of the CubeSat team, which is part of the Yale Undergraduate Aerospace Association (YUAA) that is building a satellite to be launched into low earth orbit as part of NASA’s CubeSat Launch Initiative. This 2U satellite carries a payload that will measure cosmic rays at various points in Earth orbit, along with a custom-built gravity gradient boom. When I joined the product, I was part of the Attitude Determination and Control System subteam, which had become responsible for almost all mechanical components on the spacecraft.
Based on this experience and my acceptance into the Yale First-Year Summer Research Fellowship, I was able to stay in New Haven, CT over the summer of 2022 to conduct research on the CubeSat’s detumbling algorithm. Taking on this entire project on my own was a challenge, but I was able to organize my time and leverage my resources so that I could tackle it efficiently.
While this project taught me a lot technically about MATLAB, satellite dynamics, mathematical orientation representations, and control algorithms, I think the most important lesson had to do with the challenges to make a robust and reliable real-world system. Classes have prepared me well to deal with engineering and computer science problems with clear inputs, sufficient data, and defined solutions, but this project did not include any of these. Being able to handle noisy inputs that weren’t able to fully define the CubeSat’s state taught me a lot about data processing and filtering such as the Kalman filter. Additionally, I had to use these incomplete inputs to create a “best guess” about the best way to control the magnetorquers, which are imperfect control devices because of how their torque varies based on the CubeSat’s orientation. I know that being forced to work with these challenges will help me create more robust mechanical and software systems.